티스토리 뷰
모듈1. C에서의 데이터 타입
1) 선언과 정의
- 선언(declaration)과 정의(definition)를 구분하는 기준은 "memory address binding의 유뮤"
- 어떤 대상의 이름에 대해 그에 대응하는 메모리 상의 주소가 정해진다면 그것은 정의
- 그렇지 않고 이름만 알려준다면 그것은 선언
int x; //선언함과 동시에 변수를 정의함
int x = 5; //선언함과 동시에 변수를 정의하고, 값을 할당함
int x(){ return 0; } // 선언과 동시에 정의, 호출 시 jump해야 하기 때문
struct x { int i; }
// 선언과 동시에 정의
// 구조체가 구조체 변수로 인스턴스화 할 때 어떻게 메모리가 배치될 지를 알려주는 문장
extern int x; // 선언, 다른 모듈에서 정의된 변수를 이름만 임포트
int x(); // 선언, 함수의 프로토타입 선언
struct x; // 선언, 이름만 컴파일러에게 알려주는 행위
typedef int INT; // 선언, 타입 이름 자체가 메모리 바인딩될 수 없음
2) C에서의 데이터 타입
(1) C의 배열 타입
: 정수(int), 문자(char), 부동소수(double) 등의 원시 타입은 물론, 구조체 타입의 배열도 허용
(2) 배열의 선언
- 대괄호([ ])와 함께 표기
- 일반 변수와 같은 형식으로 선언
- 예) 정수 배열 선언 - int a[100];

(3) 배열을 접근하는 연산
- 검색과 저장
- 배열 이름과 인덱스로 표현
eg) k = a[5]; a[2] = 6; - 선언된 배열의 원소 값들이 지정되기 전에는 모두 미정(undefined)
(4) 인덱스 범위(index range)
- 하단 경계와 상단 경계 사이의 값
▶ 하단 경계(lower bound): 제일 작은 인덱스 값, 항상 0
▶ 상단 경계(upper bound): 제일 큰 인덱스 값, 선언할 때 명시함
* 하단 경계와 상단 경계는 변경 불가능함 - 인덱스가 이 범위를 넘어 지칭하면, 프로그램에서 에러 발생
(5) 배열의 크기(길이)
- 상단 경계 - 하단경계 + 1
- 배열의 선언과 동시에 정의되고 고정됨
(6) 심벌 상수(symbolic constant)
- 배열 선언을 보다 융통성 있게 만들기 위해서 이용
- 배열을 상수로 초기화하는 프로그램(심벌 상수로 초기화하는 프로그램과 비교해 볼 것)
int a[100];
for(i=0; i<100; ++i)
a[i]=0;
- 배열을 심벌 상수로 초기화하는 프로그램
#define N 100
int a[N];
for (i=0; i<N; ++i)
a[i]=0;
(7) 배열의 선언과 초기화 동시에 가능
// 예시
int a[100] = {0};
float f[5] = {0.0, 1.0, 2.0, 3.0, 4.0};
// 정수형(integer) 배열의 선언과 초기화 예시
int a[4] = {0, 1, 3, -4};
int a[] = {0, 1, 3, -4};
// 문자(character) 배열의 선언과 초기화 예시
char s[] = "abc";
char s[] = {'a', 'b', 'c', '\0'}; // '\0'은 끝을 나타내는 널(null) 문자
(8) C에서의 2차원 배열
- 행(row)과 열(column)을 표현하는 2개의 인덱스로 명세
- 행 우선(row-major)으로 표현

(9) C에서의 3차원 배열
- 면(plane), 행(row), 열(column)을 표현하는 3개의 인덱스로 명세
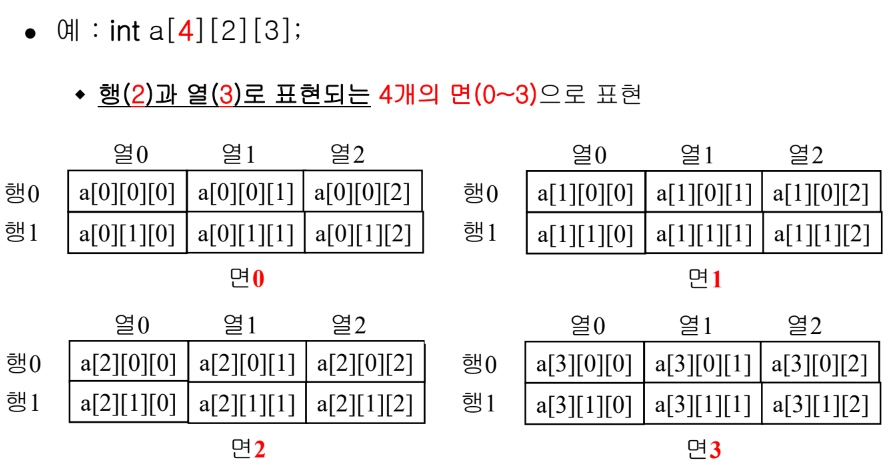
(10) 구조(struct) 데이터 타입의 배열
- Struct Data Type
- 이질 데이터(heterogeneous data)를 그룹 지어 처리
- 사용자로 하여금 데이터 타입을 정의하여 사용할 수 있도록 허용
- structure의 준말
- 몇 개의 상이한 필드 즉 멤버(member)로 구성

(11) 배열 vs 구조
- 배열(array): 타입이 같은 데이터들을 하나로 묶는 방법
- 구조체(structure): 타입이 다른 데이터를 하나로 묶는 방법



모듈2. 선형 리스트
1) 선형 리스트
(1) 리스트(list)
: 원소들의 순열(sequence)로써 원소들을 일렬로 정렬해 놓은 것
(2) 선형 리스트(linear list)
- 순서를 가진 원소들의 순열(sequence)
- 물리적 순서가 아닌 원소의 특성에 의한 논리적 순서를 의미
- 리스트는 기본적으로 순서 개념을 가지므로 선형 리스트라고 볼 수 있음
(3) 리스트의 표기

2) 리스트 ADT
(1) 리스트 처리 연산의 정의
- createList(): 초기에 공백리스트 L을 생성
- isEmpty(L): 리스트 L이 공백인지 아닌지 결정
- length(L): 리스트 L의 길이를 계산함. 여기서 리스트 길이는 리스트에 포함된 원소의 수. 공백 리스트의 길이는 0
- retrieve(L, i): 리스트 L의 i원소를 검색(1 <= i <= L의 길이)
- replace(L, x, y): 리스트 L의 원소 x를 새로운 원소 y로 대체
- delete(L, x): 공백이 아닌 리스트 L로부터 원소 x를 제거. 이때 리스트 L의 길이는 하나 감소
- insert(L, i, x): 새로운 원소 x를 리스트 L의 지정된 위치 i에 삽입. 리스트 L의 길이는 1 증가

3) 리스트의 표현
- 배열을 이용한 표현: 순차 표현 리스트
✅ 삽입, 삭제 시에 후속 원소들을 한 자리씩 밀거나 당겨야 하는 오버헤드가 치명적인 약점

모듈3. 다항식 추상 데이터 타입
1) 다항식
- 다항식(Polynomial)은 계수 X 변수^지수의 형태를 가지는 항들의 집합으로 구성된다.



2) 다항식 ADT

3) 다항식 연산의 구현
(1) 다항식 생성 ⭐
- 모든 다항식은 기본적으로 연산 zeroP()와 addTerm()을 이용해 생성할 수 있음

(2) 다항식의 표현 시 가정
- 모든 항은 지수에 따라 내림차순으로 정렬
- 모든 항의 지수는 상이함
- 계수가 0인 항은 포함하지 않음
(3) 다항식의 덧셈: 두 다항식의 항들의 지수를 비교하여 합병, 복사, 삭제를 수행
4) 다항식의 표현
(1) 모든 "차수"에 대한 "계수값"만을 배열에 저장하는 방법 - 하나의 다항식을 하나의 배열로 표현
- 문제점: Space 낭비(0인 coefficient가 매우 많아 공간 낭비)
eg) 2 * x^1000 + 1

(2) 계수와 지수가 존재하는 항만을 골라서 쌍으로 표현하는 방법

- 예제: 계수와 지수가 존재하는 항만을 쌍으로 저장하기 위한 C 선언문
#define MAX_TERMS 100 /*지수가 존재하는 term 최대수 가정*/
typedef struct{
float coef; //계수
int expon; //지수-쌍으로 저장함
} polynomial;
polynomial term[MAX_TERMS];
int avail = 0; /*다음 번 빈 슬롯의 array index 번호 유지*/
- 예제: 다항식 두 개를 하나의 배열에 표현
- 장점1: 0항이 많은 다항식(polynomial)에 유용함
- 장점2: 여러 개의 다항식을 하나의 배열에 저장 가능함
- 단점: 모든 항이 0이 아니면, memory를 최대 2배나 더 소모하게 됨(다항식의 표현법 1보다, 지수항까지도 추가로 더 저장해야 하므로)

- Total
- Today
- Yesterday
- C언어
- python
- 파이썬
- 과제안내신분
- SW생명주기
- SWLIfeCycle
- 칸토어 집합
- 백준
- 알고리즘
- 직사각형
- 다음소수
- 개발계발
- 약수
- 데이터추상화
- 4779
- 붙임성 좋은 총총이
- 배수
- 27323
- 25314
- C99
- 베라의 패션
- 배수와약수
- 25304
- 약수들의합
- 피보나치수5
- 삼각형과세변
- 브라우저
- 26069
- 점근적표기
- 브라우저뜻
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
