티스토리 뷰
1. 그래프 개념과 ADT
1) 기본 개념

(1) 정의와 용어
- Graph 자료 구조: 상하위 개념이 없는 노드와 노드들을 잇는 엣지로 구성되어 있는 자료구조이다.
- Graph에서는 모든 노드들이 관계를 가지고 있을 필요가 없어 비교적 자유로운 구조이다.

(2) 특징
- Graph는 비선형(non-linear)적이며, network model이라고도 불린다.
- 노드는 방향성이 있기도 하고 없기도 해서 각각을 '무방향성 그래프', '방향성 그래프'라고 나뉘어 부른다.
- 실생활에서는 지도나 지하철 노선도, 페이스북 친구 추천이나 e-commerce 추천 알고리즘이 있다.

2) 그래프 추상 데이터 타입
(1) 그래프의 정의

(2) 무방향 그래프: 간선을 표현하는 두 정점의 쌍에 순서가 없는 그래프
(3) 방향 그래프: 유방향 그래프 또는 다이그래프(digraph). 간선을 표현하는 두 정점의 쌍에 순서가 있는 그래프. 간선을 아크(arc)라고도 함

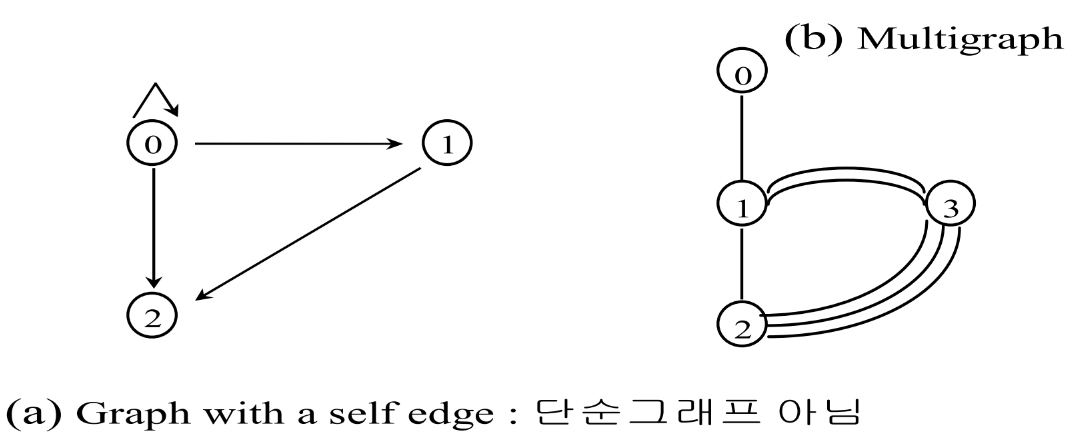
(4) 단순 그래프
- 자기 루프(self-edge, 자신을 연결하는 루프)를 허용하지 않음.
- 두 정점 사이에 최대 하나의 간선만 존재
(5) 다중 그래프
- 두 정점 사이에 둘 이상의 간선이 허용한 그래프
- 일반적으로 그래프로 취급하지 않음
(6) 완전 그래프
- 허용된 최대 수의 간선을 가진 그래프
- 정점이 n개일 때, 간선의 수는 무방향 그래프 n(n-1)/2개, 방향 그래프 n(n-1)개

(6) 부분 그래프


(7) 그래프 G에서의 정점 u로부터 v까지의 경로를 path라고 함
- 간선으로 연결된 정점의 순서 리스트 u, v1, v2, ... , vk, v
- 방향 그래프에서는 방향 경로(directed path)라고 함
- 경로의 길이(path length): 경로를 구성하는 간선의 수
- 단순 경로(simple path): 모두 상이한 간선들로 구성된 경로


(8) 사이클(cycle)
- 첫 번째 정점과 마지막 정점이 같은 단순 경로
- 무방향 그래프에서 사이클의 길이: 3 이상
- 방향 그래프에서 사이클의 길이: 2 이상

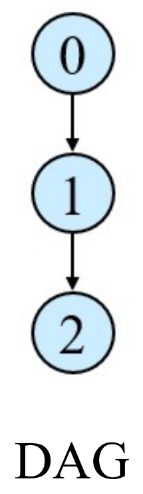

- DAG(directed acyclic graph): 방향 그래프에서 사이클이 없는 그래프
(9) 연결 그래프(connected graph): 서로 다른 모든 쌍의 정점들 사이에 경로가 있는 무방향 그래프
- 어느 한 정점에서부터 다른 어떤 정점에로의 경로 존재
- 트리(tree): 사이클이 없는 연결 그래프
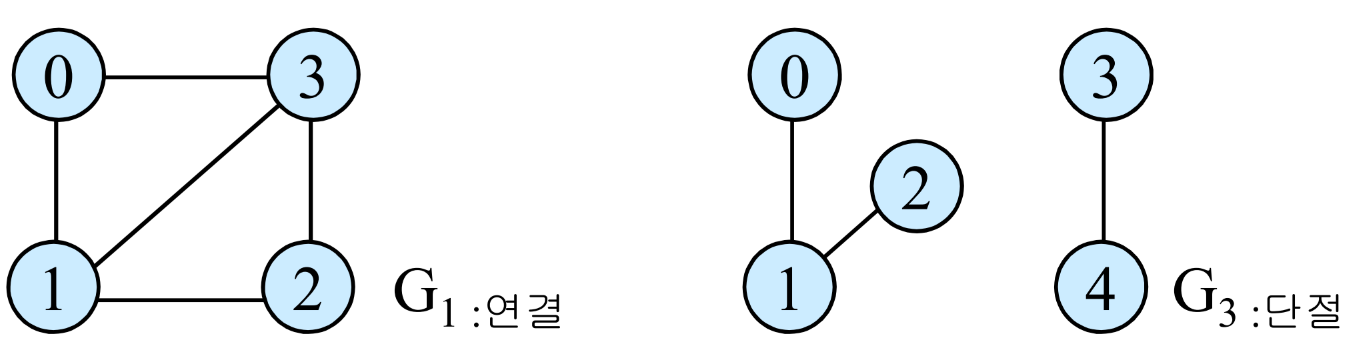
- 연결(된) 요소란?
- 최대로 연결된 부분 그래프(maximal connected subgraph)를 말함
- 최대: 최대 수의 정점과 최대 수의 간선
- 연결(된) 요소에는 정점을 추가하여 더 확장할 수 없다고 가정함 - 예) 그래프 G3: 정점 {0, 1, 2}와 {3, 4}로 구성된 2개의 연결(된) 요소
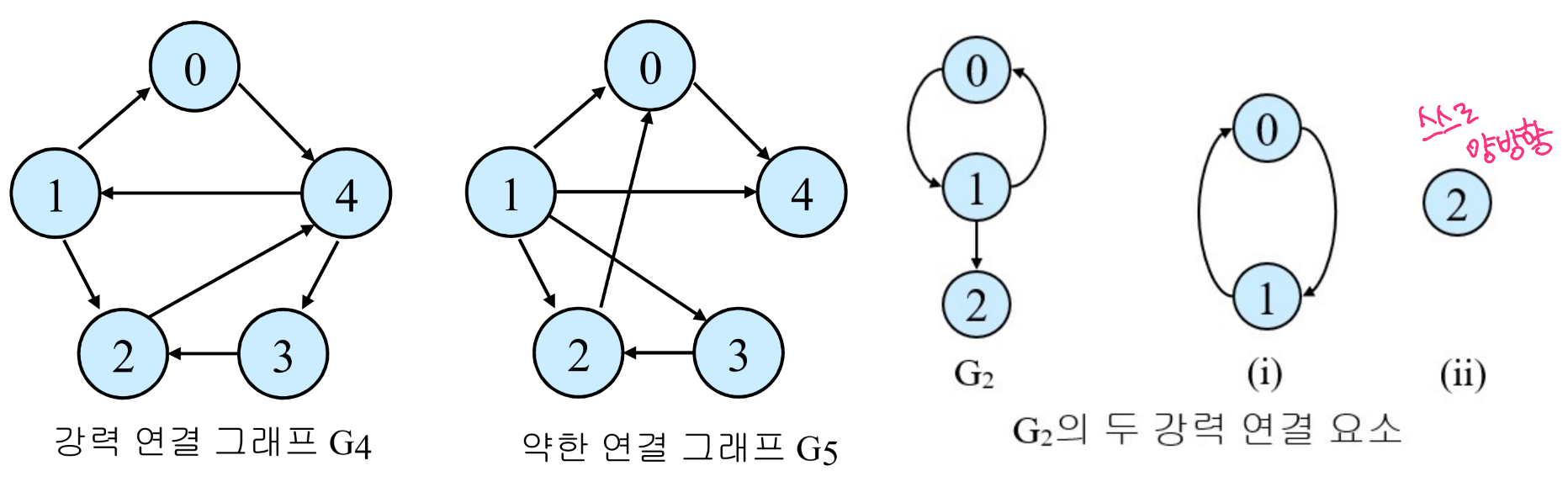
(10) 강력 연결(strongly connected)
- 방향 그래프 G에서 V(G)에 있는 서로 다른 모든 정점의 쌍 u와 v에 대해 u에서 v, 그리고 v에서 u까지의 양쪽으로 방향 경로가 존재(쌍방향)
(11) 약한 연결(weakly connected)
- 방향 그래프 G에서 V(G)에 있는 서로 다른 모든 정점의 쌍 u와 v에 대해 u에서 v, 그리고 v에서 u까지 어느 하나의 경로만 존재(단방향)
(12) 강력 연결 요소(strongly connected component)
- 강력 연결된, 최대 부분 그래프
(13) 무방향 그래프의 정점
- 정점의 차수(degree): 그 정점에 부속된 간선(edge)의 수

(14) 방향 그래프의 정점
- 진입 차수(indegree): 방향 그래프에서 정점 v로 들어오는 간선 개수
- 선행자(predecessor): 정점 v로 들어오는 간선들의 정점들. <vi, v>에서 앞쪽 vi의 수
- 진출 차수(outdegree): 방향 그래프에서 정점 v에서 나가는 간선 개수
- 후속자(successor): 정점 v에서 나가는 정점들. <v, vk>에서 뒤쪽 vk의




2. 그래프 표현
1) 그래프 표현 방법 - 그래프에서 수행하려는 연산과 응용에 따라 표현 방법을 선택
- 인접 행렬(adjacency matrix)
- 인접 리스트(adjacency list)
- 인접 다중 리스트(adjacency multilist)
2) 인접 행렬(adjacency matrix): n * n인 2차원 배열 a[n, n]로 표현
- 부속 행렬이라고도 함
- 인접 행렬로 표현하는 데 필요한 공간: n^2 비트
- 대칭 성질 활용: 무방향 그래프에서 행렬은 대칭이기 때문에 행렬의 상삼각이나 하삼각만 저장한다면 거의 반 정도의 곤간을 절약


- 인접 행렬의 정보
- 간선의 존재 여부
- 무방향 그래프 인접 행렬에서 행 i의 합은 정점 i의 차수
- 방향 그래프 인접 행렬에서
행(row) i의 합은 정점 i의 진출 차수
열(column) i의 합은 정점 i의 진입 차수

3) 인접 리스트(adjacency list)
- n개의 정점 각각에 대해 인접한 정점들을 리스트로 만듦
- 인접 리스트의 구현(연결 리스트, 순차 표현)


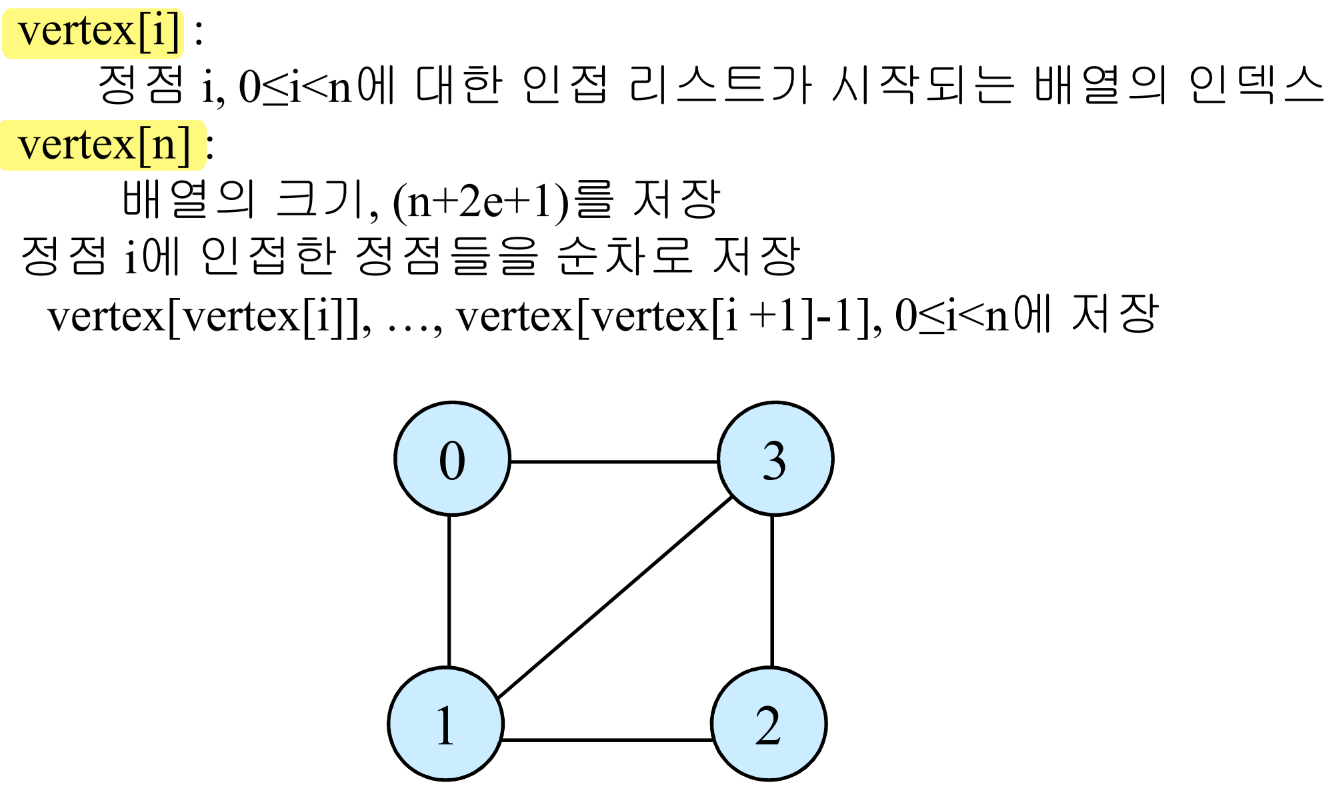
- 순차 표현(배열)으로 구현한 인접 리스트
- 각 정점 별로 인접 노드들을 순차적으로 배열에 저장
- n개의 정점과 e개의 간선을 가진 그래프: 배열 vertex[n+2e+1]로 표현




4) 인접 다중 리스트
- 인접 리스트를 다중 리스트로 표현
- 다중 리스트
- 노드들을 여러 리스트들이 공용하는 리스트
- 특정 간선에 대해 이미 접근했는 지를 표시하는 데 편리
- 간선의 두 정점 각각에 대해 인접 정점들을 리스트로 유지(하나의 간 선을 두개의 리스트가 공유)

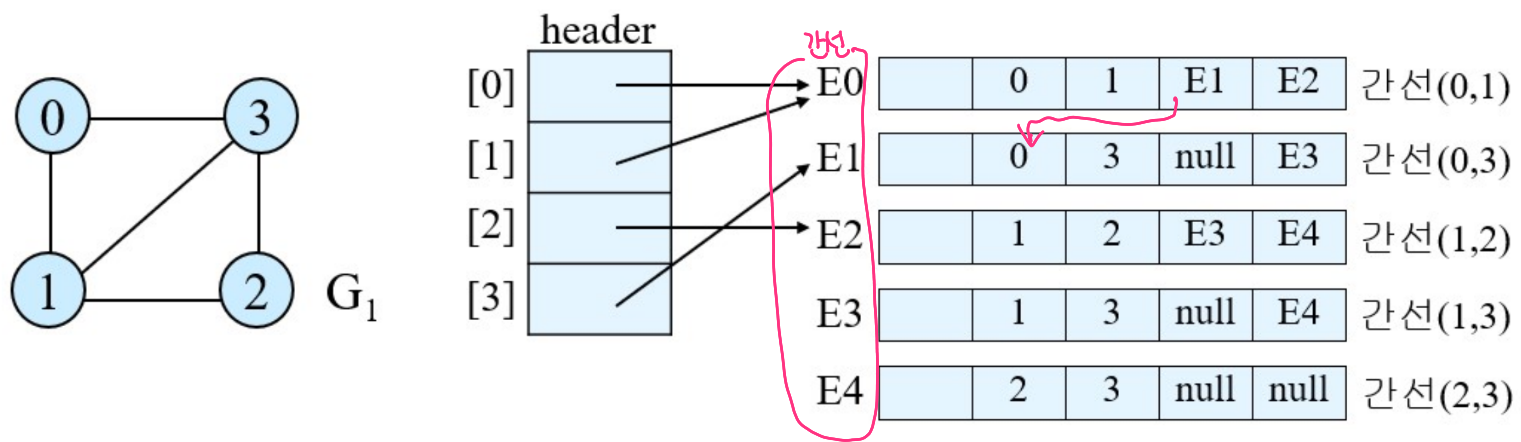
- G1에 대한 인접 다중 리스트의 식별


- Total
- Today
- Yesterday
- 백준
- 베라의 패션
- 브라우저뜻
- 개발계발
- python
- 알고리즘
- 피보나치수5
- 삼각형과세변
- 배수와약수
- 다음소수
- 약수들의합
- 붙임성 좋은 총총이
- 25314
- C99
- 점근적표기
- 4779
- SWLIfeCycle
- 27323
- C언어
- SW생명주기
- 재귀함수원리
- 25304
- 약수
- 데이터추상화
- 재귀케이스
- 직사각형
- 브라우저
- 과제안내신분
- 배수
- 파이썬
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
