티스토리 뷰
1. 이진 탐색 트리
1) Binary Search by Array
(1) Concept
Q. 서로 다른 n개의 정렬된 수가 list에 저장되어 있을 때, 특정한 값을 찾아라
A. Description of the binary search problem





2) Binary Search Trees
(1) 정의: Binary Search Tree는 탐색에 목적을 둔 binary tree이다. 본 tree는 empty일 수 있고, empty가 아닌 경우는 다음의 성질을 만족한다.
1️⃣모든 element는 서로 다른 key를 갖는다.
2️⃣Non-empty left subtree에 있는 key들은 root의 key보다 작은 값을 갖는다.
3️⃣Non-empty right subtree에 있는 key들은 root의 key보다 큰 값을 갖는다.
4️⃣left subtree와 right subtree도 역시 binary search tree이다.

(2) Binary Search Tree(BST)의 탐색법


(3) Binary Search Tree에 노드 삽입하는 방법
- unique key를 지원하므로 insert 연산 시, search 연산이 선행되어야 함
- 해당 key를 찾지 못한 경우만, 검색이 끝난 지점에 새로운 element를 삽입함

- tree_ptr forInserting_search() 설명
- tree가 비어있거나 검색 key가 이미 tree node에 있으면 NULL return,
- 없으면 search 중 만난 마지막 node에 대한 pointer return(그곳에 넣으면 된다.)

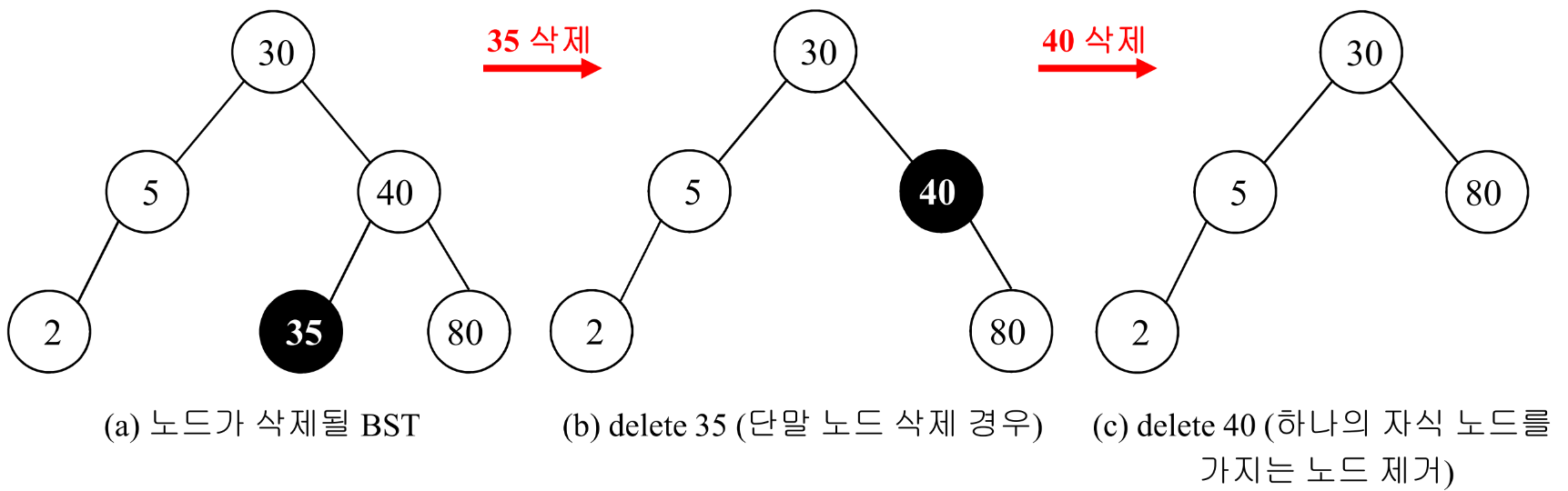
(4) Binary Search Tree에서 노드를 삭제하는 방법
- leaf node인 경우, 해당 node를 지우고 그 parent의 link를 NULL로 만든다.
- 하나의 child를 가진 non-leaf node를 delete하는 경우, 해당 node를 지우고 child node가 지워진 node를 대체한다.
- 두 개의 children을 가진 non-leaf node를 delete하는 경우, left sub-tree의 가장 큰 element나 right sub-tree의 가장 작은 element를 삭제하고자 하는 node와 대체한다.

(5) Height of a binary search tree
- 일반적인 경우(general case)
- Skewed가 아닌 BST(binary search tree)의 height는 평균 O(log2n)이다.
- ex) 만약 노드가 15개이면 대략 log2(2^4)이므로, height는 4로 볼 수 있다.
- 최악의 경우(worst case, skewed tree)
- key를 1, 2, 3, ..., n의 순으로 삽입하면, 오른쪽만 삽입이 일어나므로 binary search tree의 height가 n이 되어 height는 O(n)이 된다.
- 역순 삽입(n,,,1)도 마찬가지로 left skewed 된다.
- 그러므로, BST에서 오름이나 내림 수의 삽입은 좋지 않은 결과를 본다.
- 균형 탐색 트리(balanced search tree)
- worst case height로써 O(log2n)을 가지는 search tree이다.
- search, insertion, deletion이 O(height)에 수행된다.
- 종류: AVL tree, 2-3 tree, red-black tree 등
2. 기타 트리
1) Heaps
(1) Max tree
- 정의: max tree는 node에 있는 key value가 그 children의 key value들 보다 크거나 같다. max heap은 complete binary tree이면서 동시에 max tree이다.
- 혼돈 주의: 본 장의 heap은 tree의 일종을 말한다.(프로세스의 동적 메모리 할당을 위한 장소인 heap과 구별된다.)


(2) Min tree
- 정의: min tree는 node에 있는 key value가 그 children의 key value들보다 작거나 같다. min heap은 complete binary tree이면서 동시에 min tree이다.

(3) Insertion into a Max Heap
- 노드 삽입 위치: complete tree 구성 순서 상, 그 다음 위치이다.
- 이후 동작: 상기 삽입 위치로부터 parent 쪽 옳은 위치를 찾아 계속 올라간다.
- link 표현: 각 노드 구조에는 parent를 가리키는 link field가 있어야 한다.
- array 표현: heap은 complete binary tree이므로 배열을 사용해서 부모를 찾는 것이 편하다.

- 알고리즘
1️⃣삽입될 노드의 위치를 지정함: 가장 밑에 가장 오른쪽 단말(leaf) 노드
2️⃣새로운 키 값을 넣는다.
3️⃣parent를 통해 계속 루트 방향으로 올라가면서 키 값들을 조정한다. (i/2)
4️⃣시간 복잡도: O(트리의 깊이) -> O(log2n)

(4) Deletion from a Max Heap
1️⃣항상, Heap의 루트에서 자료를 제거하면 된다.
2️⃣자료 제거 후, 완전 이진 트리가 되도록 트리를 재조정 해야한다.
3️⃣[재조정 방법] 가장 마지막에 있는 노드를 루트로 이동해 놓고, 루트로부터 그 자식 노드들을 비교하면서 힙의 정의에 맞도록 노드들을 재조정하면서 트리를 아래 방향을 scanning 한다.(찾아가서 위치 시킨다.)
4️⃣시간 복잡도: O(트리 깊이) -> O(log2n)

2) Selection Trees
(1) 정의: Selection Tree는 binary tree이고 각 node는 자신의 children 중 작은 쪽의 값을 갖는다. 따라서 root는 최소값을 갖는다.
(2) 용어
- run: 각 ordered sequence를 부르는 이름이며, 몇 개의 record로 구성되고 key field에 따라 non-decreasing order로 정렬되어 있다.
- n: k개의 run에 속해있는 총 record의 수
- k개의 ordered sequence를 하나의 ordered sequence로 merge하는 문제
(k개의 run으로부터 첫 번째 record들을 비교하여 최소의 key를 찾는다.)
- 직접 비교 방식을 사용하면 최소값을 하나 찾기 위해 k-1번의 비교를 수행한다.
- selection tree를 이용하면 효율적으로 최소값을 찾을 수 있다.


(3) 분석

- Total
- Today
- Yesterday
- 26069
- 칸토어 집합
- 27323
- 25314
- 배수
- 배수와약수
- 4779
- 약수
- 과제안내신분
- 붙임성 좋은 총총이
- 개발계발
- 베라의 패션
- SW생명주기
- python
- SWLIfeCycle
- 삼각형과세변
- C언어
- 직사각형
- 피보나치수5
- 브라우저
- 브라우저뜻
- 점근적표기
- 다음소수
- C99
- 파이썬
- 알고리즘
- 25304
- 데이터추상화
- 약수들의합
- 백준
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
