티스토리 뷰
1. 트리 개념
1) 정의: 다음의 성질을 가진 하나 이상의 node로 이루어진 finite set이다.
- Root라고 불리우는 특정 node가 있다.
- 나머지 node들은 n개(n >= 0)의 disjoint set인 T1, T2, ... Tn으로 분할된다. 이때 각 set는 Tree이다.
T1, T2, ... Tn를 root의 subtree라고 부른다.
2) 트리는 root를 가진 acyclic graph(비순환 그래프)이고, 계층적 구조를 가진다.

3) Sample Tree로 알아보는 개념

(1) Node의 degree(자식 수) : node의 subtree 수를 말한다.
- A, D는 3
- B, E는 2
- C, H는 1
- K, L, F, G, M, I, J는 0
(2) Tree의 degree: tree에 있는 node의 degree 중 최대값
- tree의 degree는 3이다.
(3) Leaf(terminal node): degree가 0인 node를 일컫는다.
- tree에서 leaf는 K, L, F, G, M, I, J이다.
(4) Tree의 height(depth): Tree에 있는 node의 최대 level 값이다.
- 상기 tree의 height는 4이다.(높이 표기로 k나 h라는 initial을 사용한다.)
(5) Parent node: Subtree를 갖는 node는 그 subtree들의 parent이다.
(6) Children nodes: Parent를 갖는 subtree들의 root들은 그 parent node의 children이다.
(7) Sibling nodes: 같은 parent의 children을 말한다.
(8) Grand parent node: Parent의 parent node를 말한다.
(9) Grand children nodes: Children의 children nodes를 말한다.
(10) Ancestor nodes: 한 node의 ancestor는 root에서 그 node까지의 path 사에 있는 모든 node들이다.
- ex: M의 ancestor는 A, D, H
(11) Descendents nodes: 한 node의 descendents는 그 node의 subtree에 있는 모든 node들이다.
- ex: B의 descendents는 E, F, K, L
4) Forest(포리스트)
- 포리스트는 트리의 집합이다.
- n개의 서브 트리를 가진 트리에서 루트를 제거하면 n개의 분리된 트리의 집합이 된다.

5) Tree의 표현 방법
(1) List로 표현하는 방법
- 아래의 tree를 pre-order navigation하여 그 결과를 list로 표현하면, (A (B (E (K, L), F), C (G), D (H (M), I, J) ) )
- 단, root를 먼저 쓰고 subtree의 list를 나중에 쓴다.

- Linked list 구조를 이용하여 tree를 표현하는 경우 문제점
: 한 node에 있는 field 수는 branch의 개수에 따라 변하기 때문에 node structure 구현이 힘들다.
- 다음과 같이 n개의 child마다 각각 하나의 link를 둔다.


(2) Left Children-Right Sibling Tree 표현 방법
- 고정된 크기의 node 구조를 사용한다. 그러므로, 연산(operation)이 쉽다.
- 다음 그림과 같이, Node마다 두 개의 link 또는 pointer field를 가진다.



(3) Degree Two Tree Representation(표현)
- "left child - right sibling tree" 또는 "binary tree"라고 한다.
- left child - right sibling tree를 45도 시계 방향으로 회전시킨 모양이다.
- 한 node의 children을 left child와 right child로 구분한다.


(4) Tree의 표현 방법(변환 과정)


2. 이진 트리(Binary Tree)
1) 이진트리란?
(1) 정의: 이진 트리는 empty이거나, root와 2개의 disjoint binary tree(left subtree와 right subtree)로 구성
(2) 이진 트리의 ADT

2) Binary Tree의 비교
- 0개의 node를 가진 tree는 없지만, empty binary tree는 존재한다.
- Binary tree에서는 children의 order를 구분하지만, tree에서는 구분하지 않는다.
- 다음 2개의 binary tree는 다르다.

3) Skewed tree와 complete tree의 비교
(1) (left) skewed binary tree = (좌측) 편향 이진 트리
(2) complete binary tree = 완전 이진 트리

4) 이진 트리의 특성
(1) 이진 트리에 있는 node의 최대 개수
- 이진 트리의 level i 에 있는 node의 최대 개수는 2^(i-1)이다. (i >= 1, Level은 1부터)
(만약, i >= 0이라고 가정하면, = Level의 시작이 0부터라고 한다면, i에 있는 node의 최대 개수는 2^i이다.)
- 깊이(depth) k의 binary tree에 있는 node의 최대 개수는 2^k - 1이다.(k>=1)

(2) 어떤 node와 leaf node의 개수 간의 관계
1️⃣ n0은 degree 0인 leaf node의 개수이고, n1은 degree1, n2는 degree2인 node의 개수라고 하자.
전체 node 개수 n은 n = n0 + n1 + n2이다.
2️⃣ 만약 binary tree의 Branch 개수 B를 센다면, root node를 제외한 Tree T 내의 모든 node는 자기에게로 들어오는(incoming) branch를 1개씩 가지고 있다. 그러므로 B를 "Tree의 Branch(edge) 개수"라고 한다면 전체 node 개수는
n = B + 1이다.
3️⃣ Tree 전체의 Branch 개수는 B = n1 + 2n2이다. (n1 = degree1 개수, n2= degree2 개수)
4️⃣ 전체 node 개수는 n = n1 + 2n2 + 1이다.
⭐최종적으로, n0 = n2 + 1이다.

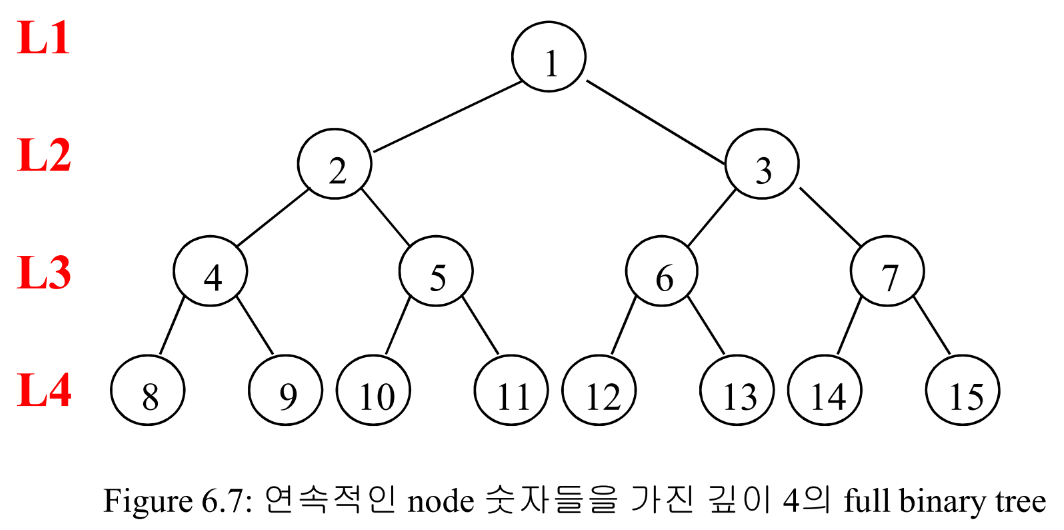
(3) depth k의 full binary tree에서, k가 0이상 일때 2^k - 1 개의 node를 갖는 depth k의 binary tree이다.
주의: 완전 이진 트리라고 해서 포화 이진 트리인 것은 아니지만, 포화 이진 트리라면 완전 이진 트리이다.
✅ 완전 이진 트리(Complete binary tree) : n개의 node들을 가지고 depth가 k인 binary tree의 node들이 depth가 k인 full binary tree의 1부터 n까지 node들과 순서가 일치한다면, 그 binary tree는 complete하다.


5) Binary Tree의 표현 방법
(1) Array로 표현하는 방법
- 1차원 array로 표현(저장)한다.
- parent, left child, right child의 위치를 쉽게 파악(검색)할 수 있다.
- 이런 표현(저장) 방법은, complete binary tree의 표현에는 공간이 낭비없이 저장되지만 편향 이진 트리의 경우에서는 빈 공간이 많아져 비효율적(문제점)이다.
- 노드의 삽입 및 삭제가 힘들다. 한 노드가 삽입되면 그 노드의 sub tree들이 모두 움직여야 한다.




▶️ 순차 표현의 장단점 정리
- 장점
- 범용성: 어떤 이진 트리에도 사용 가능
- 최적: 완전 이진 트리에서만
- 단점
- 편향 이진 트리: 배열 공간을 매우 비효율적으로 사용
-> 높이가 k인 편향 이진트리: 2^(k+1) - 1 개의 공간이 요구될 때 k + 1만 실제 사용 - 트리의 중간 내부 노드의 삭제나 삽입 시: 많은 노드들의 이동 불가피
(2) Linked List로 표현하는 방법
- Node의 parent 파악이 좀 어렵지만, 대부분의 tree 표현 응용에 적합
- 만약 Parent node를 파악하고자 한다면 node 정의에 parent field를 추가하면 된다.


- 단말 노드(left node)의 링크는 NULL을 가진다.

- 부모 노드를 알고 싶으면 "parent" field를 추가한다.

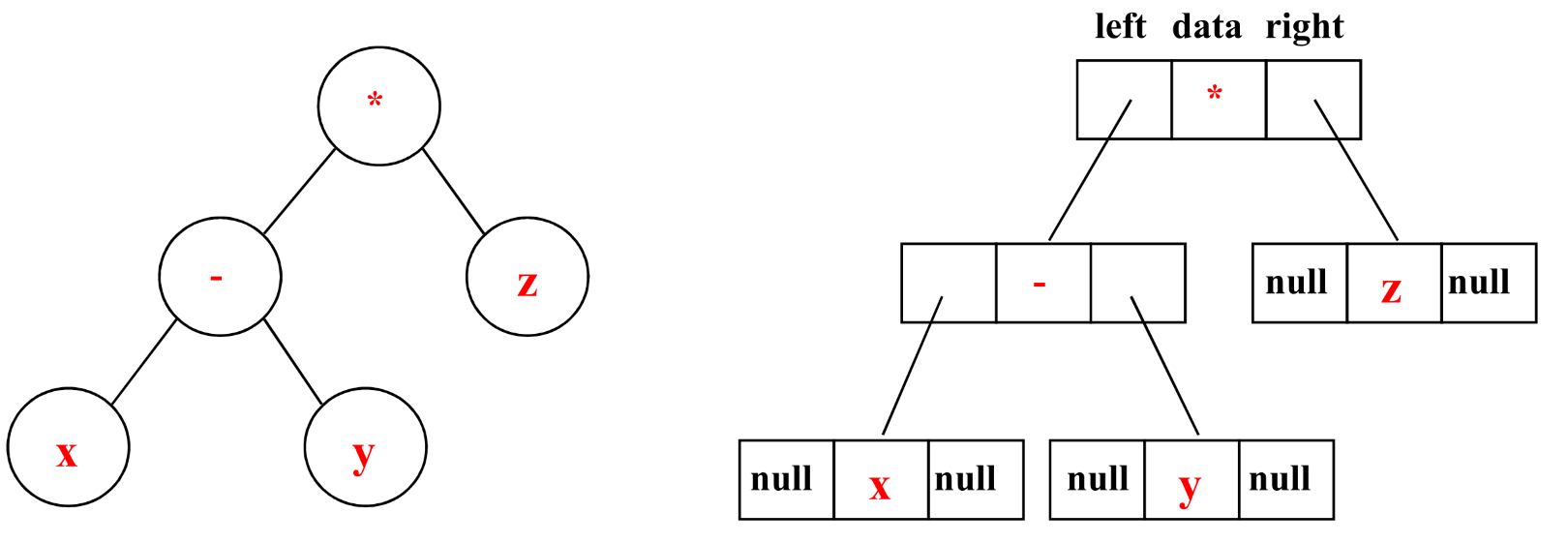
(3) 수식 이진 트리(expression binary tree)
- 수식을 이진 트리로 표현 수식 (D & C 느낌)
- Total
- Today
- Yesterday
- SWLIfeCycle
- 익스플로러
- 데이터구조
- VisualStudio
- 기계어
- javase
- 구현
- SW생명주기
- 데이터추상화
- 웹개발자
- 구글크롬
- D&C
- 개발계발
- 앱개발
- 브라우저
- 의사코드
- Abstraction
- jre
- jvm
- 비주얼스튜디오
- 바이트코드
- ADL
- 사이트만들기
- 크롬
- vscode
- 프론트엔드
- 알고리즘
- 브라우저뜻
- 프로그래밍언어
- 소스파일
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
